Computation of Integer and Algebraic Integer Relations
19th March 2021
Talk Summary
- Introduction to Integer Relations
- Computation of Classical Integer Relations
- A Brief Introduction to Algebraic Number Theory
- Algebraic Integer Relations
- Computing Quadratic Integer Relations
For convenience, we will usually think of x∈Rn and a∈Zn and say that a is an integer realtion of x.

Aside: picture proof that arctan1+arctan2+arctan3=π
and so (4,−3,4) really is an integer relation for (arctan2,π,arctan3).
History
Euclid's extended algorithm.
- am+bn=gcd(a,b) relates a, b, and gcd(a,b) by integers.
- Each iteration produces incrementally better approximation.
- Also works for real numbers (see Book X, Prop 3).
History
General case (for more than 2 numbers).
- Sought after by: Euler, Jacobi, Pincaré, Minkowski, Perron, Brun, Mahler, and others.
- None proved to work for n>3
- None adequately captured the increasing approximation property.
History
Generalisations satisfying both properties.
- First one published by Ferguson & Forcade in 1979 with extensive, unpublished notes, by Bergman.
- Several intermediate results (Ferguson & Forcade 1982, Ferguson 1986, Ferguson 1987).
- PSOS algorithm (Ferguson 1988)
- PSLQ algorithm (Ferguson & Bailey 1992)
Applications
Can see if a number α satisfies an integer polynomial by searching for integer relations of (α0,α1,…,αn)
Bailey & Ferguson used such a technique to show γ,logγ,logπ,ζ(3) and some others do not satisfy a low-degree polynomial.
Applications
Borwein Bailey Plouffe formula π=∞∑k=0(116k(48k+1−28k+4−18k+5−18k+6)) found by “inspired guessing and extensive searching using the PSLQ integer relation algorithm”
Applications
Bailey & Plouffe use PSLQ to search for (“recognise”) symbolic representations of floating point numbers.
E.g., they were able to recognise that 1.6083594219855456…≈∫∞0t7/4e−tdt=21π√216Γ(1/4) (note that the RHS can be reduced to 2116Γ(3/4))
Applications
Chamberland uses PSLQ to find relationships between functions.
There are many others. See Borwein & Lisoněk 2000 “Applications of Integer Relation Algorithms” (DOI: 10.1016/S0012-365X(99) 00256-3).
We can extend the idea to allow complex numbers.
Note that Z[i]={a+bi:a,b∈Z}
This definition encapsulates the previous one.
Talk Summary
- ✅ Introduction to Integer Relations
- Computation of Classical Integer Relations
- A Brief Introduction to Algebraic Number Theory
- Algebraic Integer Relations
- Computing Quadratic Integer Relations
When talking about integer relations in general, we use the following notation so as to encapsulate all cases.
We will use F to denote the field of numbers which we are relating and we will use O to denote the ring of integers from which the relation elements are from.
The classical cases, then, are when O=Z and F=R, and when O=Z[i] and F=C.
Let B={b1,…,bn}⊂Fn be a linearly independent set of vectors. The set L={λ1b1,…,λnbn:λ1∈O} is the lattice spanned by B. We call B the basis of the lattice L
We will sometimes refer to an O-lattice if we need to specify the integer ring explicitly.
We can represent a lattice L as a matrix by using the basis vectors as row vectors.
The lattice spanned by the vectors (1,2,0) and (3,0,4), and (0,5,6) is given by the matrix [120304056]
Note that the literature often uses column vectors instead of row vectors.
An information theoretic argument shows that in order to numerically compute an integer relation on n numbers, where the relation consists of integers with no more than d digits, then at least nd decimal digits of precision need to be used.
In the case of complex numbers and Gaussian integers, the number of digits is the number of digits in the real part, or the imaginary part, whichever is larger.
LLL
The LLL algorithm was introduced by Lenstra, Lenstra Jr, and Lovasz in 1982.
It is not an algorithm for computing integer relations directly. Instead it finds short lattice vectors
It can, however, be used to compute integer relations
LLL
Given a basis B for a lattice L, the LLL algorithm computes a basis B′=(b′1,…,b′n) such that |μi,j|≤12 for 1≤j<i≤n||b∗i+μi,jb∗i−1||2≥34||b∗i−1||2 for 1<i≤n where b∗i=b′i−∑i−1j=1μi,jb∗j and μi,j=b′i⋅b∗j||b∗j||2
LLL
To find an integer relation on x=(x1,…,xn)∈Rn we can use LLL on the lattice L:=[100⋯0Nx1010⋯0Nx2⋮⋮⋱⋯⋮⋮000⋯1Nxn] for some N∈R.
Think of this as the augmented matrix [InNx].
LLL
Elements of the lattice look like (λ1,…,λn,N(λ1x1+⋯+λnxn)) So if the λi are an integer relation for x then the last term will be 0.
We can prove that if N is large enough, then the first element of the reduced lattice must contain the integer relation.
LLL
For the complex case where n z=(z1,…,zn)∈Cn we still use the augmented lattice L:=[InNz] like we did for the real case.
However we then construct a 2nd augmented lattice [ℜLℑL−ℑLℜL] and use LLL on that lattice.
As with the real case, so long as N is large enough then the procedure must find an integer relation.
LLL
In all cases, we don't know how large to make N before we start. So we must use trial and error.
We have found, experimentally, that with numeric (floating point) calculations it is possible for N to be too large, even though the theory requires N to be “sufficiently large”.
PSLQ
The PSLQ algorithm was introduced by Ferguson & Bailey in 1988. It was later analysed by Ferguson, Bailey, and Arno in 1999
It can handle both the real and complex cases directly.
We will not discuss the details of the algorithm itself. However we will establish some facts.
PSLQ
Observe that in both the real and complex cases O forms a lattice, and that O⊂F.
Let x∈F. An integer a∈O is a nearest integer if |x−a| is maximal. A function ⌈⋅⌋:F→O is a nearest integer functino if it maps each x∈F to one of its nearest integers.
We denote by ⌈⋅⌋O if we need to be specific.
PSLQ
There are parameters: γ,ρ, and τ that must satisfy 1ρ≥|x−⌈x⌋| for all x∈F1≤τ≤ρ1τ2=1γ2+1ρ2
ρ is bounded by the integer lattice; choose to maximise 1/ρ.
γ is minimised when τ=1; choose any larger value.
τ is fixed by the choice of γ and the value of ρ.
PSLQ
Each iteration of the PSLQ algorithm finds an increased lower bound on the norm of any integer relation on the input.
The algorithm can terminate when that bound exceeds some threshold.
If the algorithm finds a relation, a then ||a||≤γn−2M where M is the norm of the smallest possible relation.
Comparing LLL and PSLQ
LLL requires more precision than PSLQ
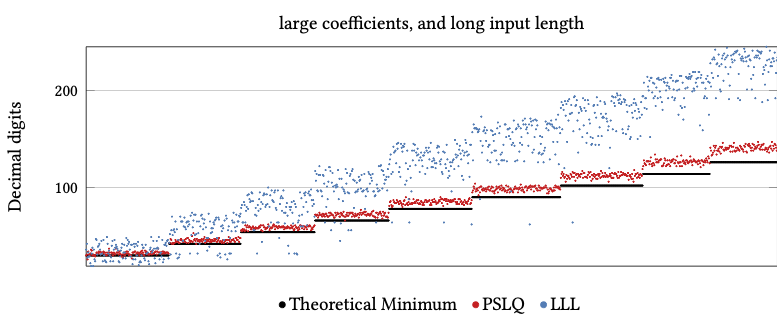
Real Integer Relation Problems
Comparing LLL and PSLQ
LLL requires more precision than PSLQ
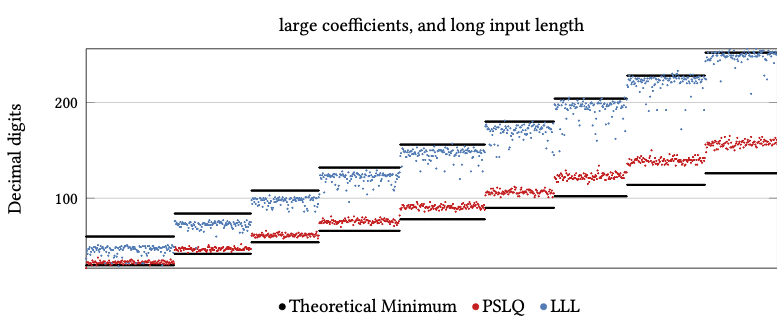
Complex Integer Relation Problems (real constants)
Comparing LLL and PSLQ
LLL requires more precision than PSLQ
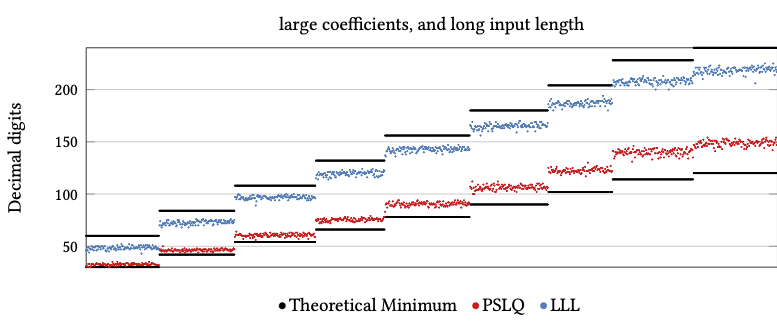
Complex Integer Relation Problems (complex constants)
Comparing LLL and PSLQ
PSLQ Required Precision (as % of theoretical min).
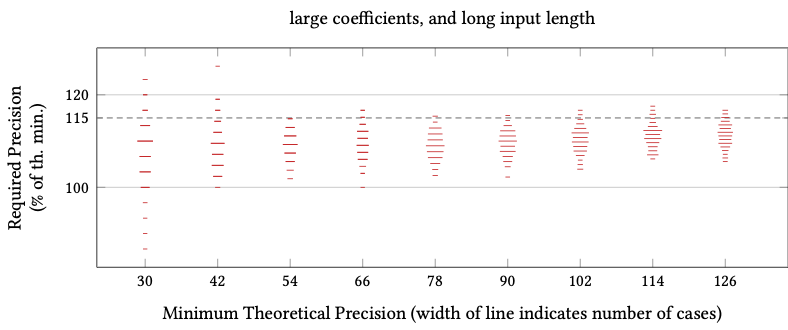
Real Integer Relation Problems
Comparing LLL and PSLQ
PSLQ Required Precision (as % of theoretical min).
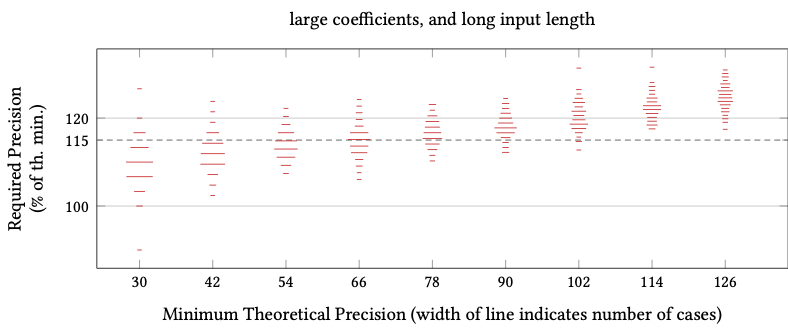
Complex Integer Relation Problems (real constants)
Comparing LLL and PSLQ
PSLQ Required Precision (as % of theoretical min).
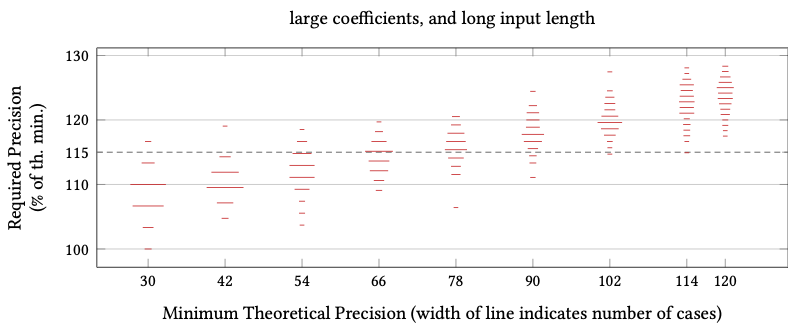
Complex Integer Relation Problems (complex constants)
Comparing LLL and PSLQ
LLL takes much more time than PSLQ
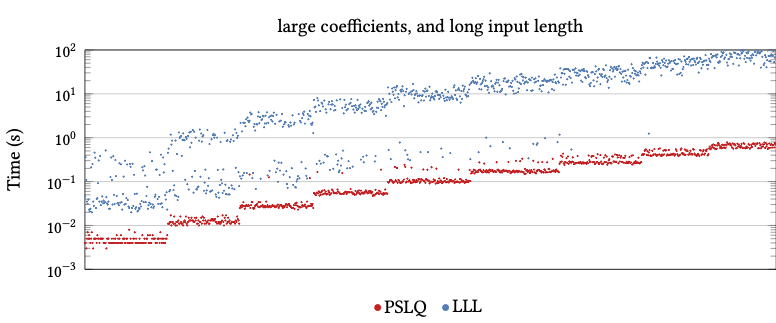
Real Integer Relation Problems
Comparing LLL and PSLQ
LLL takes much more time than PSLQ
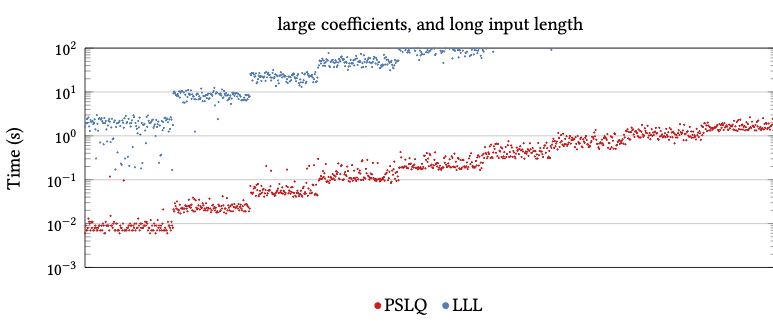
Complex Integer Relation Problems (real constants)
Comparing LLL and PSLQ
LLL takes much more time than PSLQ
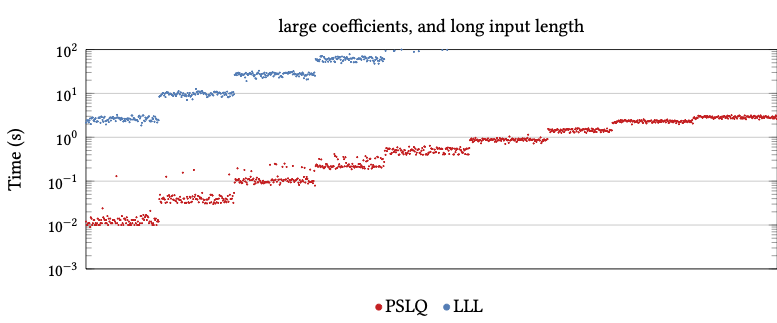
Complex Integer Relation Problems (complex constants)
Talk Summary
- ✅ Introduction to Integer Relations
- ✅ Computation of Classical Integer Relations
- A Brief Introduction to Algebraic Number Theory
- Algebraic Integer Relations
- Computing Quadratic Integer Relations
Let F be a field. If F is a subfield of some other field K (i.e., F⊆K then we call K a field extension (or, equivalently an extension field) of F.
We denote this by K:F when we need to be explicit about the base field and the extension.
Note that the literature often uses the notation K/F instead.
Let F be a field, and consider an extension field K:F. An element k∈K is said to be algebraic over F if it satisfies fnkn+⋯+f1k+f0=0 for some n∈N and fi∈F. Note that fn≠0.
For example √2 satisfies k2−2=0 and so is algebraic over the rationals.
Let D be an integral domain and consider an extension field K:F such that D⊆K. An element k∈K is said to be integeral over F if it satisfies a monic polynomial kn+dn−1kn−1+⋯+d1k+d0=0 for some n∈N and di∈D
An integral domain is a commutative ring with multiplicative identity and no non-zero elements d1,d2 with the property that d1d2=0.
Let z∈C.
We denote by Q(z) the smallest subfield of C that contains both Q and z.
We denote by Z[z] the smallest subring of C that contains both Z and z.
Note that the ring Z is often called the “rational integers” to avoid ambiguity.
We are primarily interested in extension fields of Q.
A number z∈C is an algebraic number (or simply algebraic) if it is algebraic over Q.
A number z∈C is an algebraic integer if it is integral over Z.
The ring of all algebraic integers is denoted by A.
An algebraic extension is real if K⊆R and complex otherwise.
We are primarily interested in extension fields of Q.
An extension field K:Q is an algebraic extension field (or simply an algebraic extension if every k∈K is an algebraic number.
Its ring of integers of K, denoted OK, is K∩A. We call such rings algebraic integers
We are primarily interested in extension fields of Q.
The set Q(√5) is an algebraic extension field. Its elements look like {q1+q2√5:qi∈Q}, such as 12+32101√5
The golden ratio 1+√52 is an algebraic integer of Q(√5) because it satisfies the polynomial x2−x−1=0. Similarly for 1−√52.
Quadratic Fields
We will restrict our attention to quadratic extension fields. These are fields of the form: Q(√D)={q1+q2√D:qi∈Q} wher D∈Z is square free.
Elements of these fields satisfy quadratic (or lower degree) polynomials with rational coefficients.
Quadratic Fields
The algebraic integers of a quadratic field (which we call quadratic integers) are of the form OQ(√D)=Z[ω]={m1+m2ω:mi∈Z} where ω={√D if D≡2,3(mod4)1+√D2 if D≡1(mod4)
Quadratic Fields
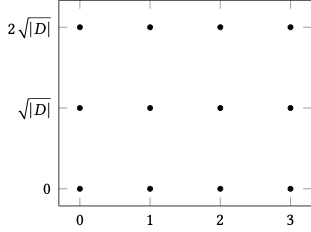
D≡2,3(mod4)
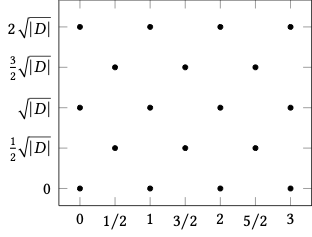
D≡1(mod4)
Quadratic Fields
Finally we mention a special class of quadratic fields.
Talk Summary
- ✅ Introduction to Integer Relations
- ✅ Computation of Classical Integer Relations
- ✅ A Brief Introduction to Algebraic Number Theory
- Algebraic Integer Relations
- Computing Quadratic Integer Relations
Relations With Algebraic Integers
Recall the definiton of an integer relation:
Relations With Algebraic Integers
We could try and replace C with an algebraic extension field, and replace Z[i] with the ring of integers of that field.
However, this won't capture the existing cases.
Relations With Algebraic Integers
We could try and replace C with an algebraic extension field, and replace Z[i] with the ring of integers of that field.
However, this won't capture the existing cases.
The fields R and C are not algebraic fields (although they are extension fields of Q ). Thus they do not have algebraic integers.
If we try to take the intersections anyway (R∩A or C∩A) we do not get correct integers.
Relations With Algebraic Integers
Instead, specify an intermediate extension field.
Let F∈{R,C} and let K be an algebraic extension field. Let O=OK.
Let x1,…,xn∈F. Integers, a1,…,an∈O are an algebraic integer relation (or a K-integer relation) of the original numbers xi if a1x1+⋯+anxn=0
Talk Summary
- ✅ Introduction to Integer Relations
- ✅ Computation of Classical Integer Relations
- ✅ A Brief Introduction to Algebraic Number Theory
- ✅ Algebraic Integer Relations
- Computing Quadratic Integer Relations
Reduction to Classical Cases
Observe that for an quadratic integer relation: (m1,1+m1,2ω)x1+⋯+(mn,1+mn,2ω)xn=(m1,1x1+⋯+mn,1xn)+(m1,2ωx1+⋯mn,2ωxn)
This suggests a way to reduce a quadratic integer relation to a classical one.
Reduction to Classical Cases
Given (x1,…,xn)∈Fn we compute (x1,…,xn,x1ω,…,xnω)∈F2n and search for a classical integer relation on that.
We recover the integer relation by taking ak+an+kω for 1≤k≤n.
This works well for real quadratic fields (i.e., when D>1). It works less well for complex quadratic fields.
Reduction to Classical Cases
In the complex case, the integers are of the form ak=mk,1+mk,2i. So when we attempt to recover the relation we get (mk,1+mk,2i)+(mk+n,1+mk+n,2i)ω after expansion and some simplification we get α1+β2i√|D|+α2i−β2√|D| for α1,β1∈Z which is not an algebraic integer in Q(√D) if α2≠0 or β2≠0.
Reduction to Classical Cases
Much of the time the reduction technique works fine, and gives good answers even in the complex cases.
When it does not work, we try two techniques to nonetheless extract a relation.
Reduction to Classical Cases
Decomposition method
We observe that α1+β2i√|D|+α2i−β2√|D| can be written as (α1+β2i√|D|)+i(α2+β2√|D|) and we have two possible algebraic integers embedded. We try extracting only these.
Reduction to Classical Cases
Conjugate Method
Given α1+β2i√|D|+α2i−β2√|D| a conjugate is α1−β2i√|D|−α2i−β2√|D|
Multiplying the number by its conjugate gives an element of OQ(√D). We multiply all elements of the relation by the conjugate of only one of the elements.
Reduction to Classical Cases
Both the methods for correcting the complex case work well in practice.
We do not have proofs that they will always be correct. It is nonetheless easy to just try them, and check the extracted relation.
Using LLL
To compute an algebraic integer n z=(z1,…,zn)∈Fn we still use the augmented lattice L:=[InNz] like we did for the real case.
However we then construct a 2nd augmented lattice. [ℜLℑLW1LW2L] and use LLL on that lattice.
Using LLL
However we then construct a 2nd augmented lattice. [ℜLℑLW1LW2L] and use LLL on that lattice.
W1xk={−√|D|ℑxk if if D≡2,3(mod4)(ℜxk−√|D|ℑxk)/2 if D≡1(mod4) W1xk={−√|D|ℑxk if if D≡2,3(mod4)(ℜxk−√|D|ℑxk)/2 if D≡1(mod4)
Using LLL
As with the other cases, so long as N is large enough then the procedure must find an algebraic integer relation.
Modifying PSLQ
We attempt to modify PSLQ while keeping the existing theory.
We simply use a quadratic integer nearest integer function, and modify the algorithm to allow us to specify the quadratic extension field we wish to use.
Modifying PSLQ
We simply use a quadratic integer nearest integer function, and modify the algorithm to allow us to specify the quadratic extension field we wish to use.
This introduces a problem: for real quadratic extension fields, the integers do not form a lattice (there is no unique nearest integer to a field element), so we cannot use the existing theory.
We restrict our attention to the complex cases, then.
Modifying PSLQ
We restrict our attention to the complex cases, then.
In these cases we have a more subtle problem.
As D increases, the parameter ρ decreases, until eventually ρ<1 making it impossible to satisfy the 1<τ≤ρ condition.
Modifying PSLQ
In these cases we have a more subtle problem.
As D increases, the parameter ρ decreases, until eventually ρ<1 making it impossible to satisfy the 1<τ≤ρ condition.
The complex quadratic fields that do not exhibit these problems are exactly: Q(√−2),Q(√−3),Q(√−7),Q(√−11)
Modifying PSLQ
As D increases, the parameter ρ decreases, until eventually ρ<1 making it impossible to satisfy the 1<τ≤ρ condition.
The complex quadratic fields that do not exhibit these problems are exactly: Q(√−2),Q(√−3),Q(√−7),Q(√−11)
These are precisely the complex quadratic norm Euclidean fields.
Modifying PSLQ
The complex quadratic fields that do not exhibit these problems are exactly: Q(√−2),Q(√−3),Q(√−7),Q(√−11)
We note that we've had surprising success with the modified PSLQ on Q(√−5),Q(√−6),Q(√−10) even though they do not fit the existing theory.
Talk Summary
- ✅ Introduction to Integer Relations
- ✅ Computation of Classical Integer Relations
- ✅ A Brief Introduction to Algebraic Number Theory
- ✅ Algebraic Integer Relations
- ✅ Computing Quadratic Integer Relations

